
Given an NFA \(N\), is it always possible to create a DFA \(M\) that recognizes the same language? If so,Įxplain how.
#HOW TO FIND FINITE STATE AUTOMATA PASSWORD#
from password recognition algorithms (to determine whether a users input is. Which of the following strings are accepted by \(N_1\)? Deterministic finite automata are finite state machines that accept or.
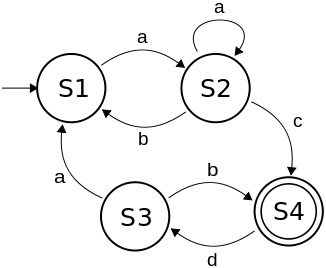
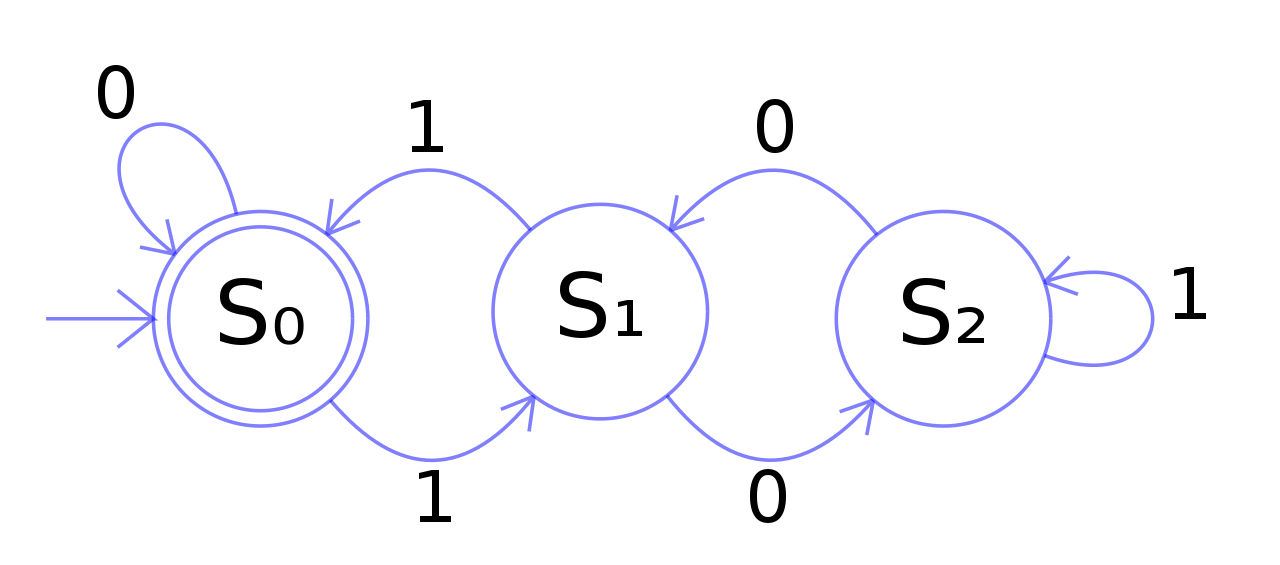
Make a table showing the transition function for \(N_1\). Which of these strings are accepted by \(N_0\)? How do we define the language recognized by an NFA? How will the graph of an NFA differ from the graph for a DFA? Here is a tabular description of the transition function for an NFA \(N_0\) with So the transition function for an NFA returns a set of states.) (The powerset of \(S\) is the set of all subsets of \(S\). Where \(S\) is the set of states, \(I\) is the input alphabet, and \(P(S)\) is the powerset of \(S\). Initially, the stack holds a special symbol Z 0 that indicates the bottom of the stack. Each transition is based on the current input symbol and the top of the stack, optionally pops the top of the stack, and optionally pushes new symbols onto the stack. For an NFA, the transition function has the form Pushdown Automata A pushdown automaton (PDA) is a finite automaton equipped with a stack-based memory. The onlyĭifference is how the transition function is specified. There is a generalization called a non-deterministic finite-state automaton or NFA. The finite state automata we have seen so far are often called deterministic finite-state automata orĭFAs. The set of bitstrings that end with two 0’s.The set of bitstrings that do not contain two consecutive 0’s anywhere.The set of bitstrings that contain two consecutive 0’s (anywhere in the string).The set of bitstrings that contain at least two 0’s.The set of bitstrings that contain exactly two 0’s.The set of bitstrings that begin with two 0’s.(We will say that such strings are accepted by \(M_0\).)įor each of the machines \(M_1, M_2, M_3\), computeįor each of the machines \(M_1, M_2, M_3\), determine the language recognized.Ĭreate automata that recognize each of the following languages. For example, in lexing HTML, input string and lexical specifications are given and we have to find lexemes. Which of these strings are in \(L(M_0)\)? A current state is determined by past states of the system and many problems are expressed in terms of finite state machine such as control applications, compilers, lexers, speech recognition or string matching. The language recognized by \(M\) (written \(L(M)\)) is defined as follows:įor each string \(x\) below, compute \(f^*(A, x)\). With transition function \(f\), start state \(s\) and final states \(F\), 9.3.3 The language recognized by a Turing Machine.9.2.1 ASCII Representations of Turing Machines.9.2 Execution of a Turing Machine program (Semantics).9.1 Definition of a 1-tape Turing Machine (Syntax).
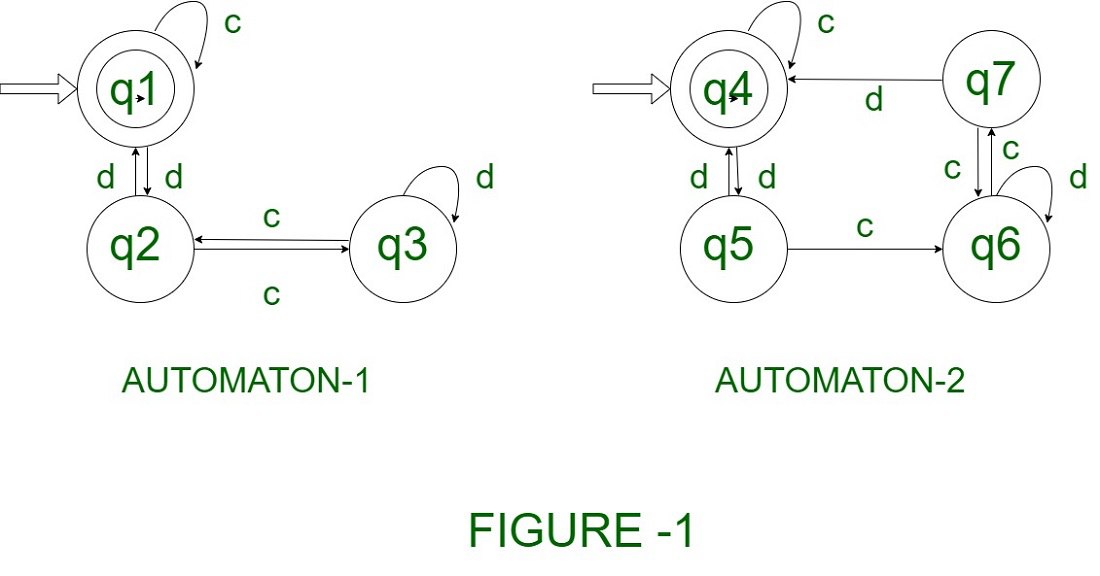
#HOW TO FIND FINITE STATE AUTOMATA FREE#
2.1 Backus-Naur Form (BNF) for Context Free Grammars.This means that the selection of the next state mainly depends on the input value and strength lead to more compound system performance. In the FSM, the outputs, as well as the next state, are a present state and the input function. How might languages be recognized mechanically? The question is of interest because if we can mechanically recognize languages like L = (w)\). The finite state machines (FSMs) are significant for understanding the decision making logic as well as control the digital systems. We have seen how regular expressions can be used to generate languages mechanically.


 0 kommentar(er)
0 kommentar(er)
